I : Formes canoniques *

II : Synthèse d’un distributeur de café *

III : Tableaux de Karnaugh *

Théorème : Toute fonction logique peut s’exprimer sous forme algébrique en n’utilisant que la somme, le produit et la négation logiques.

Nous allons voir comment, à partir de sa table de vérité, toute fonction peut s’écrire sous deux formes particulières appelées formes canoniques et utilisant des fonctions dénommées mintermes et maxtermes.

Soit un mot binaire de n variables (un problème logique avec n variables d’entrées logiques). Il existe 2ⁿ états binaires possibles pour ce mot binaire. Par conséquent, il existe 2ⁿ fonctions de ces n variables ne comportant qu’un seul ‘1’ dans leur table de vérité.

On appelle ces fonctions des mintermes et on les note m_i, i étant l’équivalent décimal de l’unique état binaire pour lequel le minterme vaut ‘1’.

Dans notre exemple, choisissons le minterme m₃.

On peut énoncer : m₃=1 ssi %CBA=%011

On obtient l’expression algébrique du minterme à partir de sa table de vérité.

Il faut noter que l’expression du minterme comprend toujours toutes les variables d’entrées soit sous leur forme directe, soit sous leur forme complémentée.

Considérons à titre d’exemple la fonction majorité S à trois variables A, B, C. Voici sa table de vérité à laquelle on adjoint la table de vérité des mintermes :

On peut donc, à partir de sa table de vérité et quelques soient la fonction et le nombre de variables d’entrée, déterminer l’expression algébrique de cette fonction, et donc d’en déduire son logigramme.

Soit un mot binaire de n variables (un problème logique avec n variables d’entrées logiques). Il existe 2ⁿ états binaires possibles pour ce mot binaire. Par conséquent, il existe 2ⁿ fonctions de ces n variables ne comportant qu’un seul ‘0’ dans leur table de vérité.

On appelle ces fonctions des maxtermes et on les note M_i, i étant l’équivalent décimal de l’unique état binaire pour lequel le maxterme vaut ‘0’.

On constate sur la table de vérité que

Cette relation permet d’obtenir l’expression de M_i à partir de celle de m_i.

On obtient l’expression algébrique du maxterme à partir de sa table de vérité.

Il faut noter que l’expression du maxterme comprend toujours toutes les variables d’entrées soit sous leur forme directe, soit sous leur forme complémentée.

Reprenons la fonction majorité S à trois variables A, B, C. Voici sa table de vérité à laquelle on adjoint la table de vérité des maxtermes :

La fonction s’exprime donc sous la forme d’un produit de maxtermes qui valent ‘0’ pour un des états d’entrée qui donnent à S la valeur ‘0’.

C’est la deuxième forme canonique.

Sous forme développée, on déduit S :

On peut donc, à partir de sa table de vérité et quelles que soient la fonction et le nombre de variables d’entrée, déterminer l’expression algébrique de cette fonction, et donc d’en déduire son logigramme.

Suivant la fonction, on aura intérêt à utiliser plutôt une forme que l’autre.

Si la table de vérité de la fonction comporte une minorité de ‘1’, mieux vaut utiliser la première forme canonique.

Si la table de vérité de la fonction comporte une majorité de ‘1’, mieux vaut utiliser la deuxième forme canonique.

Dans la plupart des cas, on préférera utiliser la première forme.

Un tableau de Karnaugh est constitué de cases (ou régions minimales) associées à chacune des combinaisons d’entrée de la fonction représentée. Il possède donc 2ⁿ cases pour une fonction de n variables.

Un tableau de Karnaugh est conçu de manière à permettre d’effectuer commodément des simplifications sur l’expression de la fonction.

C’est une forme particulière de la table de vérité.

La forme utilisée est la suivante :

Dans ce tableau, la case repérée * est associée à la combinaison %DCBA=%1101.

On remarque que les combinaisons correspondant à deux cases adjacentes ne différent que pour une seule des variables d’entrée. Par exemple :

La case marquée d’une * correspond à la combinaison %DCBA=%1101.

Les 4 cases marqués d’un . lui sont toutes adjacentes. Leurs combinaisons associées sont :

%DCBA=%0101, %DCBA=%1001, %DCBA=%1100, %DCBA=%1111.

Chaque case possède 4 cases adjacentes, dont les combinaisons associées ne différent que par une et une seule variable.

On peut noter dans la case la combinaison d’entrée associée. On indique alors quelle combinaison (ici %DCBA).

La représentation d’une fonction par tableau de Karnaugh s’obtient en dessinant un tableau de la dimension correspondant au nombre de variables de la fonction puis en hachurant (ou grisant, …) chacune des cases associées à une combinaison d’entrée pour laquelle la fonction vaut ‘1’.

La construction du tableau peut être faite directement ou à partir de la table de vérité.

Un minterme n’ayant qu’un seul ‘1’ dans sa table de vérité, il n’y aura qu’une seule case hachurée dans son tableau de Karnaugh.

Inversement, un tableau de Karnaugh n’ayant qu’une seule case hachurée représente un minterme.

Pour une fonction de n variables d’entrées, les produits possibles de ces variables d’entrée (sous forme directe ou complémentée) se répartissent en :

Produits de 1 variable, de 2 variables, de 3…. De n-1 variables, de n variables (mintermes).

Les produits de deux variables : par exemple S=/A.B

Son tableau de Karnaugh est :

Il est constitué de deux cases adjacentes. Une telle région est appelée région de taille 2.

Inversement, une région de taille 2 dans un tableau de Karnaugh à trois variables représente un produit de 2 variables.

Pour un produit d’une seule variable, par exemple, S=B

Le tableau de Karnaugh de S est :

Il est constitué de 4 cases hachurées adjacentes.

Une telle région est appelée région de taille 4.

Inversement, une région de taille 4 dans un tableau de Karnaugh à trois variables représente un produit d’une seule variable.

De manière générale, avec n variables, on admettra :

Un produit de n variables représente un minterme, il correspond à une case hachurée unique.

Un produit de n-1 variables correspond à une région de taille 2.

La première s’obtient directement : chaque case hachurée représentant un minterme, on effectue un OU des mintermes correspondants aux cases hachurés.

On cherchera à établir la fonction sous forme d’une somme de produits les plus courts possible de variables d’entrée sous forme simple ou complémentée.

Pour cela, on essaie à partir du tableau de Karnaugh, de déterminer les régions de taille maximum, en recouvrant toutes les cases hachurées. Une région de taille 4 donne un produit plus simple qu’une région de taille 2.

Si l’on reprend l’exemple de la fonction majorité à trois variables :

Il faut trouver les régions de taille la plus grande possible. On peut réaliser les groupements ci-dessus :

On trouve 3 régions de taille 2 (aucune région de taille 4 possible). Toutes les cases hachurées sont contenues dans ces régions.

S=S1+S2+S3.

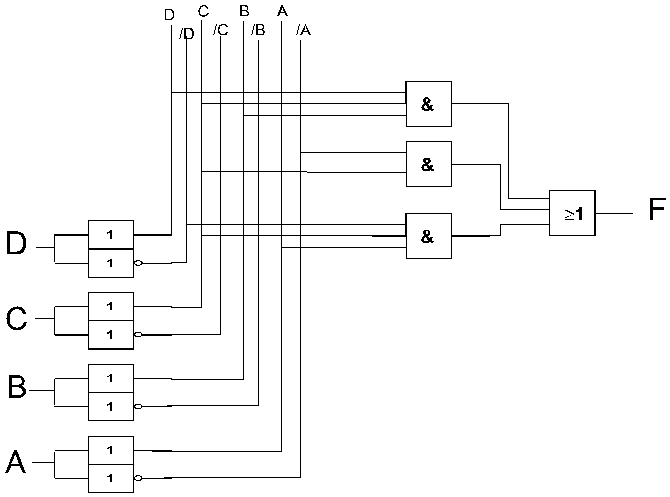
Lorsqu’on synthétise une fonction combinatoire à l’aide des tableaux de Karnaugh, suivant la méthode décrite ci-dessus, on établit un logigramme dit en " trois couches ".

On a vu que cette méthode donnait comme expression algébrique de la fonction une somme de produits des variables d’entrées ou de leur complément.

Quelle que soit la fonction et le nombre de variables d’entrées, la structure du circuit sera toujours :

• Un étage d’entrée, composé de OUI et de NON, fournissant à la fois une fonction buffer (amplification, éventuellement isolation par " trois états ") et la fonction complémentation. Cet étage fournit 2n variables, qui sont les n variables d’entrée et leur complément.
• Un étage de ET utilisant les 2n variables de l’étage précédent
• Un étage de OU combinant les produits de l’étage précédent pour donner la sortie du système.

Cette structure présente plusieurs avantages :

• Une structure standard, facilitant la réalisation technique et l’utilisation de composants programmables
• Un temps de propagation minimal.
• Un même temps de propagation pour toutes les branches du circuit (sorties)

Soit la fonction F(D,C,B,A) dont voici la table de vérité :

Construisons le tableau de Karnaugh de la fonction F à partir de sa table de vérité :

Il y a un groupement de taille 4 (donc un produit de 2 variables) et deux groupements de taille 2 (un produit de 3 variables).

Leurs expressions sont :

/A.C, B.C.D et D.A./C

D’après le tableau de Karnaugh, on déduit que l’expression minimale de F est :

F = /A.C + /D.A.C + B.C.D