
Circuits de Calcul
I : Addition en binaire naturel *
I.2 : Structure du demi-additionneur *
I.2.a : Table de vérité *
I.2.b : logigramme *
I.3 : Structure de l’additionneur *
I.3.a : Table de vérité *
I.3.b : Logigramme *
I.4 : Additionneur n bits *
I.4.a : Principe *
I.4.b : Performances *
I.4.c : Alternative *
II : Soustraction en binaire naturel *
II.1.a : table de vérité *
II.1.b : Logigramme *
II.2 : Structure du soustracteur *
II.2.a : table de vérité *
II.3 : Soustracteur n bits – n bits *
III : Addition en binaire signé *
III.2 : Structure d’un additionneur-soustracteur n bits *
III.2.a : synoptique *
III.2.b : Changeur de signe *
III.2.c : Logigramme *
IV : Gestion du dépassement *
IV.2 : Définition du dépassement *
IV.3 : Détection du dépassement *
IV.3.a : Expression de V+ *
IV.3.b : Expression de V- *
IV.3.c : Expression de V *
V : Comparaison binaire *
V-2 : Comparaison en binaire naturel *
V-3 : Comparaison en binaire signé *
VI : Multiplication *
VI-2 : Multiplieur combinatoire *
VI-3 : Multiplieur séquentiel *
VI-4 : Autre multiplieur *
I : Addition en binaire naturel
Rappel : en décimal, addition " à la main " :
13
+ 11
24
En binaire naturel :

Le bit de retenue est appelé carry en anglais.
Une demi-addition est une addition bit à bit (0+1=1,0+0=0,1+0=1,1+1=(1)0) sans retenue.
Une addition est une addition bit à bit avec retenue.
La retenue d’une addition bit à bit est utilisée dans l’addition bit à bit de la " colonne " suivante.
I.2 : Structure du demi-additionneur
En entrée du demi-additionneur on trouve un mot binaire de 2 bits %B0A0.
En sortie du demi-additionneur on a le résultat de l’addition S0 et le bit de retenue C1.
A0 |
B0 |
S0 |
C1 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
On déduit de cette table que :
S0 = A0Å B0
C1 = A0.B0
Rappel : Définition du OU Exclusif : AÅ B=(A+B)./(A.B)
I.3 : Structure de l’additionneur
Un additionneur bit à bit permet, dans une " colonne ", de déterminer la somme " locale " et la retenue, à partir des bits de la colonne et de la retenue de l’addition précédente.
(An; Bn, Cn) à (Sn, Cn+1)
An |
Bn |
Cn |
Sn |
Cn+1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
On en déduit les expressions algébriques suivantes :
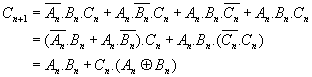
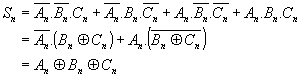
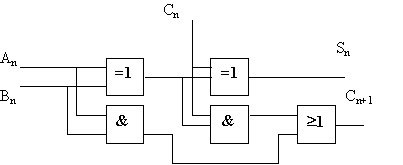
On obtient donc un additionneur 1 bit + 1 bit en mettant en série deux demi-additionneurs ; on obtient la retenue finale en effectuant un " ou " des deux demi-retenues.
Remarque : un demi-additionneur est un additionneur pour lequel la retenue précédente Cn est systématiquement nulle.
En effectuant " à la main " une addition binaire, on voit le principe de sérialisation du calcul.
Pour un additionneur n bits + n bits, on a donc besoin d’1 demi-additionneur et de n-1 additionneurs.
Ce type d’additionneur est appelé à propagation. Le temps de parcours du circuit est proportionnel à n. En pratique, le temps de calcul risque d’être important assez vite.
On peut construire un additionneur n bits de manière différente : il suffit d’établir directement la fonction complète des 2n bits d’entrée vers les n+1 bits de sortie ; pour cela on peut utiliser les tableaux de Karnaugh par exemple. On obtient ainsi des circuits en " trois couches " qui conduisent à un temps de propagation rapide, quel que soit n. Par contre, le nombre de " portes " devient vite très important.
II : Soustraction en binaire naturel
La soustraction en binaire naturel reste, dans le principe, très proche de l’addition.
(A0, B0) à (D0, C1)
A0 |
B0 |
D0 |
C1 |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
On déduit de la table de vérité :
D0 = A0Å B0
C1 = /A0.B0
On remarque que le demi-soustracteur ne différe du demi-additionneur que par la complémentation du A sur la retenue.
II.2 : Structure du soustracteur
(An, Bn, Cn ) à (Dn, Cn+1)
An |
Bn |
Cn |
Dn |
Cn+1 |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
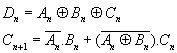 On déduit de
la table de vérité les expressions algébriques suivantes :
On déduit de
la table de vérité les expressions algébriques suivantes :
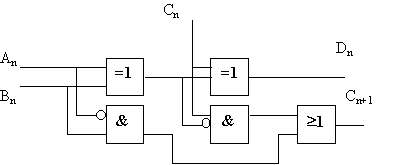
Un soustracteur est constitué de deux demi-soustracteurs placés en série, la retenue finale étant obtenue par un " ou " des demi-retenues.
II.3 : Soustracteur n bits – n bits
De même que pour l’additionneur, on sérialise le problème.
Pour un soustracteur n bits, il faut donc n-1 soustracteurs et 1 demi-soustracteur.
On a 2n variables d’entrée, et n+1 variables de sortie.
Les mêmes remarques sur les performances que pour l’additionneur sont valables.
III : Addition en binaire signé
III.1 : Remarques préliminaires
III.2 : Structure d’un additionneur-soustracteur n bits
On désire un dispositif réalisant une addition ou une soustraction en fonction d’une consigne X : addition si X=0, soustraction si X=1.
Cela revient à changer le signe de la deuxième opérande quand X=1.
On a vu que la négation d’un nombre en binaire signé était son complément à 2, c’est à dire son complément auquel on ajoute 1.
On pose Y=A si X=0, Y=/A si X=1.
Voici sa table de vérité :
| X | A | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
On remarque que Y=XÅ A.
On applique donc bit à bit sur B un ou exclusif, mais la complémentation est incomplète.
Il reste à ajouter 1 à l’ordre le plus faible quand X est non nul.
On doit donc rajouter X.
Voici le logigramme d’un additionneur n
bits en binaire signé :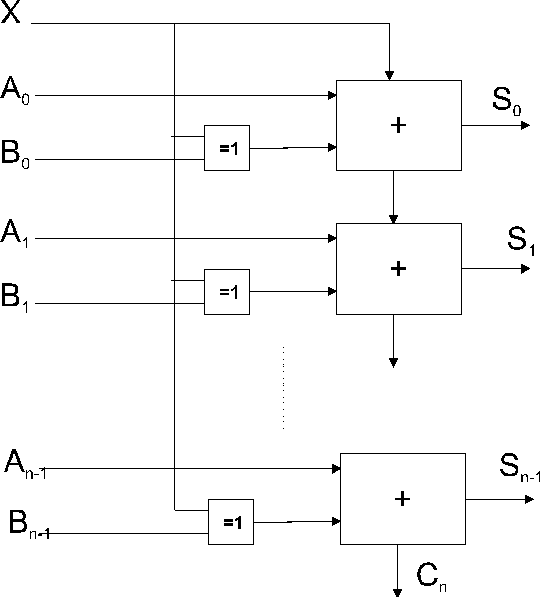
Cette fonction possède 2n+1 variables d’entrée, et n+1 variables de sortie.
On a vu que pour les entiers signés en binaire, le format était très important. En effet, le bit de signe étant le bit de poids fort, il faut connaître le nombre de bits du codage. En effet, le nombre : 1000 0000 signifie –128 sur 8 bits, mais 128 sur un format supérieur (16 bits par ex) et 0 dans un format inférieur (4 bits par ex).
En binaire signé sur 4 bits, on peut coder les nombres entiers compris entre –8 et +7.
Examinons l’addition –3 + (-6) : (-9 en décimal) :
1101
+ 1010
1 0111
Le résultat sera %0111, c’est à dire +7. Le résultat est bien sûr complètement faux, puisque positif et non égal à –9. Bien sûr, c’est normal puisque –9 ne peut être codé sur 4 bits. (On remarque qu’un cinquième bit est noté dans l’addition). La retenue n’est pas significative.
Examinons maintenant l’addition 7+1 :
0111
+ 0001
0 1000
Le résultat est : %1000, -8 en décimal ! L’erreur commise est inacceptable ! Et pourtant, la retenue est nulle ! On remarque le problème de dépassement.
Il convient donc de donner l’information ‘dépassement ‘ pour indiquer un résultat faux.
IV.2 : Définition du dépassement
Lors d’une addition en binaire signé, il y a dépassement si :
IV.3 : Détection du dépassement
La présence ou non d’un dépassement est matérialisée par un bit V (oVerflow, dépassement en anglais). Ce bit est présent dans un registre du processeur.
On note V+ le dépassement lors d’une addition (X=0).
On note V- le dépassement lors d’une soustraction (X=1).
On rappelle qu’un nombre en binaire signé est positif si son MSB est nul, et négatif si le MSB est égal à 1.
Pour des nombres sur n bits :
![]()
Pour des nombres sur n bits :
![]()
Pour des nombres sur n bits :
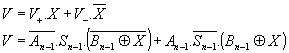
Pour comparer deux nombres entre eux, on effectue leur soustraction et on analyse le résultat obtenu.
V-2 : Comparaison en binaire naturel
On a donc :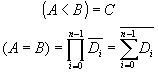
V-3 : Comparaison en binaire signé
On a donc :
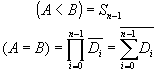
La multiplication est une opération beaucoup plus complexe que l’addition.
Exemple : sur 4 bits.
En entrée, les nombres sont codés sur 4 bits.
En binaire naturel, leur étendue est de 0 à 15. En multipliant deux nombres, on arrive au maximum à 15*15=225. Il faut 8 bits pour coder 225. (27=128, 28=256).
En binaire signé, leur étendue est de –8 à +7. Les produits " extrèmes " sont :
-8*-8 = +64
-8*+7=-56
On a besoin donc d’une étendue de –56 à +64. Avec 8 bits on code de –64 à +63.
Il faut donc deux fois plus de bits pour coder le résultat d’une multiplication que pour ses opérandes. En binaire signé, il y a un dépassement (-8*8) possible.
VI-2 : Multiplieur combinatoire
On dresse la table de vérité du multiplieur. A l’aide d’une méthode comme les tableaux de Karnaugh, on réalise la synthèse des équations logiques du multiplieur.
Avantages : calcul rapide (si réalisation " en trois couches ", très rapide).
Inconvénients : taille du circuit très importante.
On procède par additions successives ou par décalage de bits.
Avantages : taille du circuit restreinte, peu de " portes "
Inconvénients : temps de calcul.
On observe une multiplication " à la main ".
On remarque n " produits partiels ", qui sont en fait des " et ".
On additionne les n " produits partiels " pour avoir la multiplication.
Ce circuit nécessite donc un (ou plusieurs) additionneur(s).